noyau d'une application linéaire de R³

A - L'application est bijective
Soit l'application linéaire f définie sur ³ et à valeur dans ³ par :
f (x ; y ; z ) = (-x + 2y + 5z ; x + 2y + 3z ; -2x + 8y + 10z )
on veut déterminer le noyau Ker f de cette application c'est à dire l'ensemble des vecteurs (x ; y ; z) de ³ tels que :
il suffit alors soit de résoudre le système suivant :
f (x ; y ; z ) = 0

le noyau de cette application est réduit au vecteur nul (0 ; 0 ; 0) de ³ ,
Ker f = { (0 ; 0 ; 0) }
vous pouvez également calculer le déterminant de la matrice associée à f :

si ce déterminant n'est pas nul , sans faire d'autre calcul vous pouvez dire que l'application f est bijective et que son noyau est réduit au vecteur nul .
ici on a :
det A = 32 ( voir ce lien ) donc on retrouve bien que le noyau de cette application est réduit au vecteur nul (0 ; 0 ; 0) de ³ .
si ce déterminant est nul , il faudra chercher une base du noyau.
B - L'application n'est pas bijective
Soit l'application linéaire f définie sur ³ et à valeur dans ³ par :
f (x ; y ; z ) = (x +3y + 5z ; 2x + 4y + 6z ; 3x + 7y + 11z )
on veut déterminer le noyau Ker f de cette application c'est à dire l'ensemble des vecteurs (x ; y ; z) de ³ tels que :
il suffit alors soit de résoudre le système suivant :
f (x ; y ; z ) = 0

le noyau de f est l'ensemble des triplets ( z ; -2z ; z) = z(1 ; -2 ; 1) où z décrit l'ensemble des réels, cet ensemble est engendré par le vecteur de composantes
( 1 ; -2 ; 1) , il est de dimension 1 ( 1 vecteur ) .
Ker f = { z(1 ; -2 ; 1) où z }
vous pouvez utiliser la matrice associée à f :

Il apparaît que det A = 0 ( voir ce lien ) donc l'application n'est pas bijective.
déterminons le rang de la matrice A, ce qui va nous renseigner sur la dimension du noyau.
En utilisant les même propriété que pour simplifier le calcul d'un déterminant nous allons déterminer une matrice semblable à A :

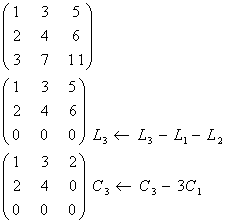
on a pu annuler qu'une seule ligne , donc le rang de la matrice est 2 et la dimension du noyau est de dim(³) - rang A = 3 - 2 = 1.
cela vient du théorème suivant :
Thèorème du rang :
lorsque l'espace vectoriel E est de dimension finie :
dimension du noyau + rang de l'application = dimension de E.
Ker f + rang f = dim E
il suffit de trouver un vecteur qui engendre le noyau , en regardant les colonnes colonne de la matrice on voit que :

Ker f = { z(1 ; -2 ; 1) où z }